Objectives / Rules
- Complete the grid so that every row and column contains every number exactly once.
- The symbols indicate which squares are numerical neighbours (e.g. 1
2, 34, 21). - Rule 1 – if there is a symbol, the numbers are neighbours (and differ by 1).
- Rule 2 – if there is NOT a symbol, the numbers are NOT neighbours.
See the Walkthrough or Notes below for extra information.
What are the symbols for?
The symbols are double arrows that point to two numbers that are neighbours of each other.
e.g. 12, 32, 34.
Click or move your mouse over the puzzle to see the answer.
Walkthrough
Step 1
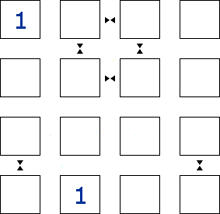
This is the start of the puzzle.
Solve this puzzle for yourself at the same time.
This example highlights the importance of the lack of a neighbour symbol.
This is the start of the puzzle.
Solve this puzzle for yourself at the same time.
This example highlights the importance of the lack of a neighbour symbol.
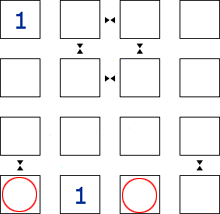
Step 2
Because the <1> has no neighbour symbols, these squares in this row cannot be <2>.
Because the <1> has no neighbour symbols, these squares in this row cannot be <2>.
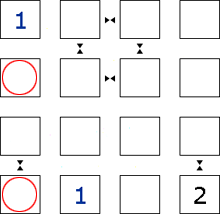
Step 3
Because neither <1> has a neighbour symbol, these squares in this column cannot be <2>.
Because neither <1> has a neighbour symbol, these squares in this column cannot be <2>.
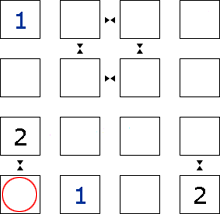
Step 4
Because the <2> has a neighbour symbol, this square must be either <1> or <3>. However, there is already a <1> in both the row and column, therefore this square is the <3>.
Because the <2> has a neighbour symbol, this square must be either <1> or <3>. However, there is already a <1> in both the row and column, therefore this square is the <3>.
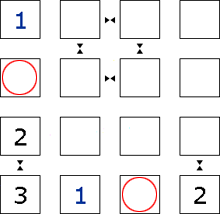
Step 5
This row and column can now be completed.
This row and column can now be completed.
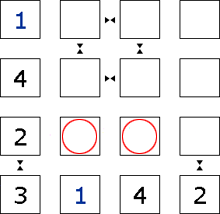
Step 6
As neither the <2> nor the <4> has a neighbour symbol, these squares cannot be <3>.
As neither the <2> nor the <4> has a neighbour symbol, these squares cannot be <3>.
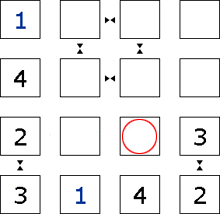
Step 7
This square cannot be <4>, and the row can be completed.
This square cannot be <4>, and the row can be completed.
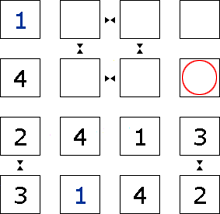
Step 8
There is already a <4> in this row, so the <4> for this column can't go in this square, and the column completes.
There is already a <4> in this row, so the <4> for this column can't go in this square, and the column completes.
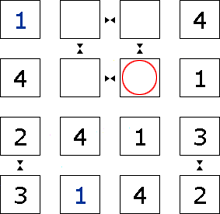
Step 9
Because the <1> has no neighbour symbol, this square cannot be <2>. The puzzle quickly completes.
Because the <1> has no neighbour symbol, this square cannot be <2>. The puzzle quickly completes.
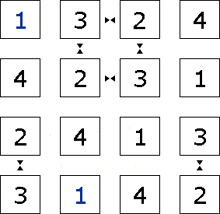
Step 10
the completed puzzle.
the completed puzzle.
Notes
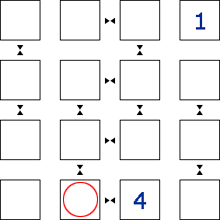
This square has to be <3> because of the neighbour symbol next to the <4>.
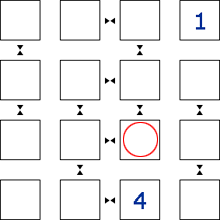
This square CANNOT be <3> because there isn't a neighbour symbol next to the <4>.
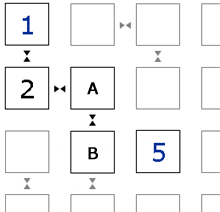
Because of the given <2> and the neighbour symbol, A can only be <1> or <3>.
Therefore B could be <2> or <4> – however, B can't be 4 as the <5> has no neighbour symbol.
So B must be <2> (and A is either <1> or <3>).
Therefore B could be <2> or <4> – however, B can't be 4 as the <5> has no neighbour symbol.
So B must be <2> (and A is either <1> or <3>).
Note: BrainBashers has a Dark Mode option – I recommend not using your browser's dark mode or extensions for BrainBashers