Puzzle 1
Three teachers were discussing how long they had been teaching.
Alex and Billie had been teaching for a total of 36 years.
Charlie and Billie had been teaching for a total of 22 years.
Charlie and Alex had been teaching for a total of 28 years.
How long had each been teaching?
Puzzle Copyright © Kevin Stone
workings
hint
answer
print
Share link – www.brainbashers.com/puzzle/zkld
Hint
If we look at all of the clues, each person appears exactly twice.
Answer
Alex had been teaching for 21 years.
Billie had been teaching for 15 years.
Charlie had been teaching for 7 years.
Reasoning
If we look at all of the clues, each person appears exactly twice.
So the total of the three clues gives us two lots of Alex + Billie + Charlie = 36 + 22 + 28 = 86.
So, Alex + Billie + Charlie = 43 years.
In each clue we are given two of the people, so we can use this to find the missing person:
Charlie and Billie had been teaching for a total of 22 years, which means that Alex must be: 43 - 22 = 21 years.
Charlie and Alex had been teaching for a total of 28 years, which means that Billie must be: 43 - 28 = 15 years.
Alex and Billie had been teaching for a total of 36 years, which means that Charlie must be: 43 - 36 = 7 years.
Reasoning With Algebra
Let Alex = A, Billie = B and Charlie = C, then:
[1] A + B = 36
[2] C + B = 22
[3] C + A = 28
If we use [3] - [2] we have:
[4] A - B = 6
If we use [1] + [4] we have:
2A = 42
A = 21
By [1] B = 15. By [3] C = 7.
Puzzle 2
This puzzle is called 'Mamma's Age', and is taken from 'Amusements In Mathematics' by Henry Ernest Dudeney (1917).
Tommy: "How old are you, mamma?"
Mamma: "Let me think, Tommy. Well, our three ages add up to exactly seventy years."
Tommy: "That's a lot, isn't it? And how old are you, papa?"
Papa: "Just six times as old as you, my son."
Tommy: "Shall I ever be half as old as you, papa?"
Papa: "Yes, Tommy; and when that happens our three ages will add up to exactly twice as much as to-day."
Tommy: "And supposing I was born before you, papa; and supposing mamma had forgot all about it, and hadn't been at home when I came; and supposing--"
Mamma: "Supposing, Tommy, we talk about bed. Come along, darling. You'll have a headache."
Now, if Tommy had been some years older he might have calculated the exact ages of his parents from the information they had given him. Can you find out the exact age of mamma?
workings
hint
answer
print
Share link – www.brainbashers.com/puzzle/zpyu
Hint
The answer isn't a whole number of years, and algebra might be required.
Answer
29 years 2 months.
Reasoning #1
This answer is taken directly from the original book.
The age of Mamma must have been 29 years 2 months; that of Papa, 35 years; and that of the child, Tommy, 5 years 10 months. Added together, these make seventy years. The father is six times the age of the son, and, after 23 years 4 months have elapsed, their united ages will amount to 140 years, and Tommy will be just half the age of his father.
Reasoning #2
Here's my answer, with a little algebra.
If we call Tommy T, Mamma M and Papa P we can see that:
"our three ages add up to exactly seventy years" gives us:
(1) T + M + P = 70
"Just six times as old as you" gives us:
(2) P = 6 x T
In an unknown number of years (Y) "Shall I ever be half as old as you" gives us:
(3) P + Y = 2 x (T + Y)
and "our three ages will add up to exactly twice as much as today" gives us:
(T + Y) + (M + Y) + (P + Y) = 140
which can be written as
(4) T + M + P + 3Y = 140
We can see from (4) and (1) that
3Y = 70
so
(5) Y = 70 ÷ 3
Using (2) and (5) in (3) we have
P + Y = 2 x (T + Y)
6 x T + 70 ÷ 3 = 2 x (T + 70 ÷ 3)
4 x T = 70 ÷ 3
(6) T = 70 ÷ 12
We can now use (6) in (2) to see that:
P = 6 x T
P = 6 x 70 ÷ 12
P = 70 ÷ 2
And using the values for T and P in (1) we have:
T + M + P = 70
70 ÷ 12 + M + 70 ÷ 2 = 70
Multiply throughout by 12 to give:
70 + 12 x M + 420 = 840
12 x M = 840 - 420 - 70
12 x M = 350
M = 350 ÷ 12
So:
Tommy = 70 ÷ 12 = 5.83333 = 5 years 10 months.
Papa = 70 ÷ 2 = 35 = 35 years.
Mamma = 350 ÷ 12 = 29.1666 = 29 years 2 months.
Puzzle 3
What number is...
...three-quarters of eight-ninths of one-half of 2001?
Puzzle Copyright © Kevin Stone
workings
hint
answer
print
Share link – www.brainbashers.com/puzzle/zrtd
Hint
Can the fractions be simplified?
Answer
667.
Reasoning
3 8 1
— of — of — of 2001
4 9 2
which simplifies to:
24
—— of 2001
72
which simplifies to:
1
— of 2001
3
Giving 667.
Puzzle 4
How many squares, of any size, can you find on this chessboard that do not contain a Rook?
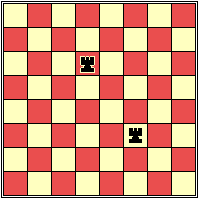
Puzzle Copyright © Kevin Stone
workings
hint
answer
print
Share link – www.brainbashers.com/puzzle/zrzl
Hint
How many 2x2 squares are there?
Answer
128.
Reasoning
There are 62 squares of size 1 x 1.
There are 41 squares of size 2 x 2.
There are 18 squares of size 3 x 3.
There are 6 squares of size 4 x 4.
There is 1 square of size 5 x 5.
A total of 62 + 41 + 18 + 6 + 1 = 128.
next >

