Help - Killer Sudoku

Objectives / Rules

Complete the grid such that every row, every column, and every 3 x 3 block contains the numbers from 1 to 9.
Every cage has a little clue in the corner, and the numbers in each cage must add to the clue.
A number can't appear more than once in a cage (which is different to Calcudoku).

Note: if you see blank white squares in the puzzle, it's not loaded correctly. Please refresh the page to reload.

See the Basic Ideas and the Walkthrough below for extra tips and tricks, and don't forget that these are Sudoku-type puzzles, and the information on the Sudoku help page might help you as well. I have provided a page that shows possible combinations

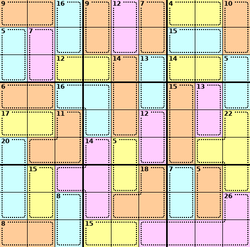
What are the numbers for?
These tell you the sums of the digits in each cage, where a cage is a collection of two or more squares inside a dotted enclosure.

Click or move your mouse over the puzzle to see the answer.

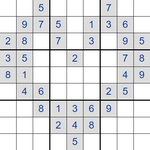
Basic Ideas

Normal Sudoku rules, tips, tricks and techniques apply.

Every row, column, and 3 × 3 block must contain the digits 1 to 9.

The puzzle is broken down into cages, and the small number in the corner tells you the sum of the digits in a cage, 15 = 1 + 5 + 9.

Pencil marks are the easiest way of keeping track of possible values for each square. Here we see the cage clue of 16, which can only be 7+9 or 9+7 (it can't be 8+8), so we enter both digits into the squares. I have provided a page that shows possible combinations to help you reduce the number possible values for some cages, for example a two square cage of 4 can only be <13> in some order.

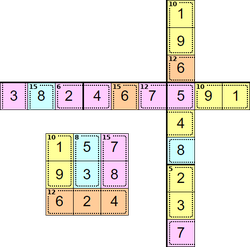
Walkthrough

Step 1
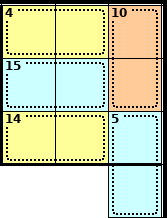
This is the start of a section of a puzzle.

Solve this puzzle for yourself at the same time.

Step 2
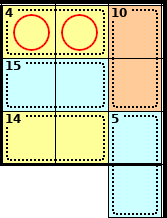
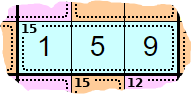
A 4 cage can only be solved using 1 + 3 (as 2 + 2 isn't allowed).

Step 3
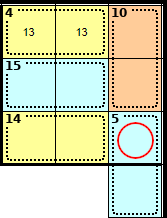
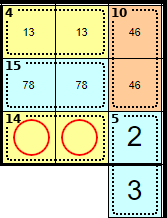
There are 4 cages entirely in the 3 × 3 block, and these 4 cages add to 4 + 10 + 15 + 14 = 43. We know that all nine squares of a block add to 45, therefore this square is <2>. The other square in the 5 cage is therefore <3>.

Step 4
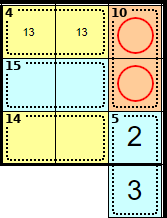
These squares can't be 1 + 9 (because the <1> belongs to the 4 cage), 2 + 8 or 3 + 7 (because of the 5 cage). Therefore these squares are 4 + 6.

Step 5
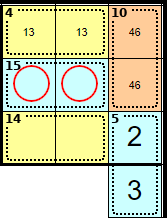
These squares can't be 6 + 9 (because of the 15 cage), and are therefore 7 + 8.

Step 6
Therefore these square are 5 + 9.

Step 7
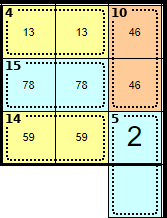
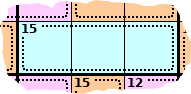
This section will hopefully help with the rest of the puzzle.

Note: BrainBashers has a Dark Mode option. For BrainBashers, I'd recommend not using your browser's built-in dark mode, or any dark mode extensions (sometimes you can add an exception for a specific website).