Puzzle 17
Snail Race - Logic Puzzles
At last year's BrainBashers snail race, 10 fine snails completed the tabletop course.
Predictably, as per every year, the results mysteriously went missing.
However, various spectators remembered the following snippets of information:
Orange Berry lost to Zebra Wings.
Zebra Wings beat Orange Berry, Frog Flippers and Apple Pie.
Fizzy Pop lost to Minty Mouth, Orange Berry and CD Player.
Frog Flippers beat Windy Hill, CD Player and Orange Berry.
Top Hat lost to CD Player, Kipper Slippers and Apple Pie.
CD Player beat Top Hat and Fizzy Pop.
Apple Pie lost to Zebra Wings and Orange Berry.
Kipper Slippers lost to Apple Pie and Frog Flippers.
Frog Flippers beat Fizzy Pop, Minty Mouth and CD Player.
CD Player lost to Frog Flippers, Kipper Slippers and Apple Pie.
Top Hat beat Fizzy Pop and Windy Hill.
Minty Mouth lost to Windy Hill and Orange Berry.
Windy Hill lost to Apple Pie and CD Player.
Can you work out who finished where?
Puzzle Copyright © Kevin Stone
Share link:

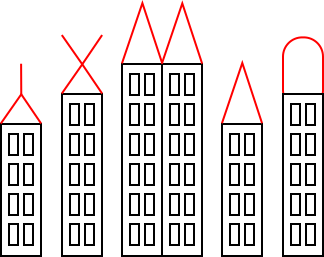
Puzzle 18
Can you add two lines to complete this sequence of towers?

Note: this puzzle is not interactive, and cannot be clicked.
Puzzle Copyright © Lloyd King
Share link:
Puzzle 19
In each of these sentences, can you replace the missing number.
The number is written as a word (e.g. five, twenty-four, thirty-three), and each sentence is correct after the replacement.
This sentence contains {?} X.
Slightly trickier, this sentence contains {?} R's.
Even trickier, this sentence contains precisely {?} E's.
This sentence has exactly {?} letters.
This sentence, hopefully, contains {?} letters, one hyphen, five commas, and four Y's.
To finish, if this sentence had a T removed, it would contain {?} letters!
Puzzle Copyright © Kevin Stone
Share link:
Puzzle 20
Take a word from the first column, and a word from the second column.
You will now have 6 lots of eight letters, and each of these eight letters is an anagram of something that lives in water.
dish leek
tray shoe
raft sign
cram golf
ears fern
loud hiss
Puzzle Copyright © Kevin Stone
Share link:
Note: BrainBashers has a Dark Mode option – I recommend not using your browser's dark mode or extensions for BrainBashers