Puzzle 5
Can you find every occurrence of the word SEPTEMBER that appears in this grid (horizontally, vertically, or diagonally)?
The hint will reveal the number of times it occurs, but where are they?

Note: this puzzle is not interactive, and the letters cannot be selected.
Puzzle Copyright © Kevin Stone
www.brainbashers.com
Puzzle 6
Below you will find 15 well-known six-letter words, with only their endings remaining.
Can you find the words?
---rnt
---few
---ryo
---yme
---rak
---urd
---ynx
---mpi
---hom
---ovy
---lpt
---hma
---voy
---web
---mur
Puzzle Copyright © Kevin Stone
www.brainbashers.com
Puzzle 7
Can you find the country hidden in the following sentence:
After falling off the roof at work, Dale's pain was relieved by an ice compress.
Puzzle Copyright © Kevin Stone
www.brainbashers.com
Puzzle 8
Can you find every occurrence of the word AUGUST that appears in this grid (horizontally, vertically, or diagonally)?
The hint will reveal the number of times it occurs, but where are they?
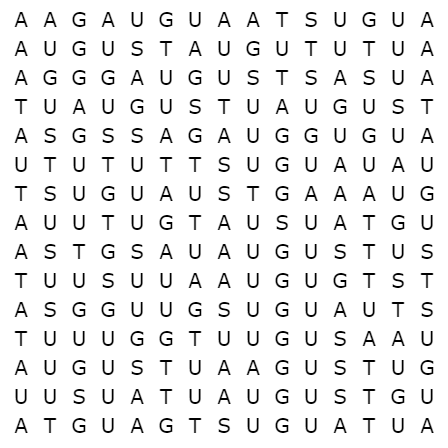
Note: this puzzle is not interactive, and the letters cannot be selected.
Puzzle Copyright © Kevin Stone
www.brainbashers.com

